今天看了poj1753，想了半天没有思路，就去看了一下题解《POJ 1753 Flip Game（状态压缩+BFS）解题报告》。这个题如果没之前没遇到过类型题的话，很难想到方法。先上题。

题目描述

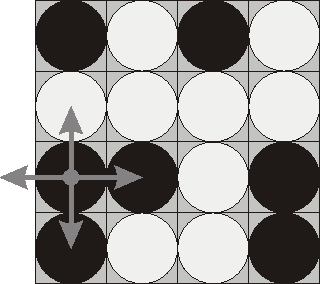
如图，题目描述如下：
给定4*4的一个棋盘，并给定某一状态的黑白棋子状态和翻转规则，问最少经过多少步可以翻转到全黑或者全白？

翻转规则如下：
若选定一个坐标 (i,j) 的棋子进行翻转，那么该棋子邻边（上下左右）的棋子也一并会翻转（也就是共5个棋子进行了翻转）。黑色变白色，白色变黑色。

思路

主要讲一下解题思路，至于状态压缩的细节，以及如何进行位运算，作者blue的题解报告《POJ 1753 Flip Game（状态压缩+BFS）解题报告》已经介绍地很详细了，就不再重复造轮子了。

之所以一开始没有想到解题方法，是因为根本没有往bfs方向上想，因为如果进行状态遍历的话，时间复杂度是 $O(n^n)=O(16^{16})$，感觉会爆。不过看网上的题解说这个复杂度不大，囧,一看我就是小白。

  • 首先将初始状态加入队列q; … (1)
  • 若q不为空；则(3) …(2)
  • 从队列中取出元素，依次翻转16个位置的棋子。如果翻转位置i的棋子之后，达到最终状态，则结束算法，返回步数。否则将该状态加入队列q，并翻转位置i+1,判断是否达到最终状态，直至遍历完16个位置。返回(2) …(3)

我咋感觉描述地这么晦涩。。。直接附上原作者代码吧。。明晚再ac替换代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <cstdio>
#include <queue>
using namespace std;

const int size = 4;
const int dir_num = 4;
struct info {
    int value;    // 状态值 
    int step;    // 步数
};
int dir[dir_num][2] = {
        {-1, 0}, {0, 1},
        {1, 0}, {0, -1},
    };
int pos[size*size];    // 16 种翻转状态
bool vis[1<<(size*size)];    //标记某状态是否已出现过

// 判断某个位置是否在棋盘内
bool Judge(int x, int y) {
    if(x>=0 && x<size
        && y>=0 && y<size)
        return true;
    else return false;
}

// 预处理 16 种翻转状态
void Initialize() {
    for(int i=0; i<size; ++i) {
        for(int j=0; j<size; ++j) {
            // i*size + j 即编号
            int value = 1 << (i*size + j);
            for(int k=0; k<dir_num; ++k) {
                int next_x = i+dir[k][0];
                int next_y = j+dir[k][1];
                if(Judge(next_x, next_y))
                    // 加上 1<<(编号) 即可将此位置设置为1
                    value += 1 << (next_x*size + next_y);
            }
            pos[i*size+j] = value;
        }
    }
}

int BFS(int value) {
    queue<info> q;
    info s = {value, 0};
    q.push(s);
    vis[s.value] = true;
    while(!q.empty()) {
        info f = q.front();
        q.pop();
        // 盘面全黑 (0) 或全白 (2^16-1) 时结束，返回步数
        if(f.value==0 || f.value==(1<<(size*size))-1)
            return f.step;
        // 搜索全部 16 个位置
        for(int i=0; i<size*size; ++i) {
            // 通过异或运算得到翻转后的状态
            info next = {f.value^pos[i], f.step+1};
            if(!vis[next.value]) {
                q.push(next);
                vis[next.value] = true;
            }
        }
    }

    return -1;    // 无法到达目标状态，返回 -1
}

int main(int argc, char const *argv[]) {
    Initialize();
    char str[5];
    int value = 0;
    for(int i=0; i<size; ++i) {
        scanf("%s", str);
        // 计算起始状态的值
        for(int j=0; j<size; ++j) {
            if(str[j] == 'w')
                value += 1 << (i*size + j);
        }
    }
    int ans = BFS(value);
    if(ans >= 0) printf("%d\n", ans);
    else printf("Impossible\n");
    
    return 0;
}