正太分布简介
本文将介绍概率论与数理统计中的一个重要分布—正太(高斯)分布。在机器学习中,很多算法都假定其先验分布是正太分布。几乎可以说,正太分布是最常用的分布。
1. 概率密度函数和概率分布函数
概率密度函数和概率分布函数都是基于随机变量的。在概率论中,随机变量分为离散型随机变量和连续型随机变量。
如果随机变量的值可以都可以逐个列举出来,则为离散型随机变量。如果随机变量X的取值无法逐个列举则为连续型变量。
概率论的核心在于研究随机变量的概率分布。为了理解更加直观,我们首先介绍离散型随机变量的概率密度函数和概率分布函数。
1.1 离散型随机变量的概率密度函数和概率分布函数
概率函数是描述随机变量取值概率的函数。以掷骰子为例,其概率函数可以描述为:
$$p_i=P(X=a_i) , i=1,2,3,4,5,6$$
在上式中,X是一个随机变量表示在掷骰子的值,$a_i$表示掷骰子所有可能的取值,$p_i$表示一次实验中掷骰子取值为$a_i$的概率,而P就是我们所说的概率函数。在掷骰子这个事件中,$p_i=\frac{1}{6}$。
离散型随机变量的概率分布依然在描述随机变量取值的概率,不过它更侧重于分布,例如下表:
| X | $x_1$ | $x_2$ | … | $x_n$ |
|---|---|---|---|---|
| $p_i$ | $p_1$ | $p_2$ | … | $p_n$ |
上表很清晰地描述了随机变量X所有取值的概率分布,实际上,概率函数和概率分布本质上都是在描述随机变量的概率,只不过是两种不同的形式。需要注意的是,概率分布必须要所有取值的概率分布。
概率分布函数有时也被叫做累积概率函数或累积分布函数。设离散型随机变量X的概率函数是$P \lbrace X=X_k \rbrace =p_k$,则概率分布函数F(x)为:
$$F(x)=P(X \leq x)=\sum_{x_k \leq x} {p_k}$$
由于F(x)是X取$\leq x$的诸值$x_k$的概率之和,所以F(x)也叫累积概率函数。
1.2 连续型随机变量的概率密度函数和概率分布函数
连续型随机变量的概率函数和概率分布函数和在离散型随机变量中的定义类似。连续型随机变量的概率函数也叫概率密度函数。这里可以讲一下“密度函数”的由来。在陈希孺老师所著的《概率论与数理统计》描述如下:
“密度函数”这个名词的来由可以解释如下,取定一个点x,则按分布函数的定义,事件$\lbrace x\lt X \leq x+h\rbrace$的概率(h>0 为常数),应为F(x + h) - F(x),所以,比值[F(x+h) - F(x)]/h可以解释为在x点附近h这么长的区间(x,x+h)内,单位长所占有的概率。令 $h \to 0$,则这个比的极限,即 $F’(x)=f(x)$,也就是在x点处(无穷小区段内)单位长的概率,或者说,它反映了概率在x点处的“密集程度“。你可以设想一条极细的无穷长的金属杆,总质量为1,概率密度相当于杆上个点的质量密度。
也就是
$$P(a \leq X \leq b)=F(b)-F(a)=\int_a^b {P(x)} ,{\rm d}x$$
2. 正太分布
2.1 正态分布
若连续性随机变量X的的概率密度函数为
$$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad -\infty <x<+\infty$$
其中$\mu, \sigma (\sigma>0)$为常数,则称X服从参数为$\mu, \sigma$的正太分布或高斯分布,记为$X\sim N(\mu, \sigma^2)$。
f(x)具有以下性质:
- f(x)关于$x=\mu$对称;
- 当$x=\mu$时,f(x)取得最大值;
- x离$\mu$越远,f(x)的值越小。这表明对于同样长度的区间,当区间离$\mu$越远,X落在这个区间的概率越小。
X的分布函数为
$$F(x)=\frac{1}{\sqrt{2\pi}\sigma}\int_{ -\infty }^x {e^{-\frac{(t-\mu)^2}{2\sigma^2}} ,{\rm d}t}$$
特别地,当$\mu=0, \sigma=1$时,称随机变量X服从标准正太分布,其概率密度和分布函数分别用$\varphi(x), \Phi(x)$表示,即:
$$\varphi(x)=\frac{1}{\sqrt{2\pi}}e^{-t^2/2}$$
$$\Phi(x)=\frac{1}{\sqrt{2\pi}}\int_{ -\infty }^x {e^{-t^2/2} ,{\rm d}t}$$
易知
$$\Phi(-x)=1-\Phi(x)$$
2.2 标准正太分布
一般,若$X\sim N(\mu, \sigma^2)$,我们只需要通过一个线性变换就可以将其转为标准正太分布。
引理: 若$X\sim N(\mu, \sigma^2)$,则$Z=\frac{X-\mu}{\sigma} \sim N(0,1)$
证: $Z=\frac{X-\mu}{\sigma}$的分布函数为
$$P\lbrace Z\leq x\rbrace=P \lbrace \frac{ X-\mu}{\sigma} \leq x \rbrace= P\lbrace X\leq \mu + \sigma x\rbrace$$
$$=\frac{1}{\sqrt{2\pi}\sigma}\int_{ -\infty }^{\mu + \sigma x} {e^{-\frac{(t-\mu)^2}{2\sigma^2}} ,{\rm d}t}$$
令$\frac{t-\mu}{\sigma}=u$,则
$$P\lbrace Z\leq x\rbrace = \frac{1}{\sqrt{2\pi}}\int_{ -\infty }^x {e^{-u^2/2} ,{\rm d}u}=\Phi(x)$$
由此可知$Z=\frac{t-\mu}{\sigma}\sim N(0,1)$。
于是,若$X\sim N(\mu, \sigma^2)$,则它的分布函数可写成
$$F(x)=P\lbrace X\leq x\rbrace=P\lbrace \frac{X-\mu}{\sigma} \leq \frac{x-\mu}{\sigma}\rbrace=\Phi(\frac{x-\mu}{\sigma})$$
对于任意区间$(x_1,x_2]$,有
$$P\lbrace x_1 < X \leq x_2\rbrace=P\lbrace \frac{x_1-\mu}{\sigma} < \frac{X-\mu}{\sigma} \leq \frac{x_2-\mu}{\sigma} \rbrace$$
$$=\Phi(\frac{x_2-\mu}{\sigma})-\Phi(\frac{x_1-\mu}{\sigma})$$
此外,由$\Phi(x)$的函数表可知
$$P\lbrace \mu-\sigma < X \leq \mu + \sigma\rbrace=\Phi(1)-\Phi(-1)=2\Phi(1)-1=0.6826$$
$$P\lbrace \mu-2\sigma < X \leq \mu + 2\sigma\rbrace=\Phi(2)-\Phi(-2)=2\Phi(2)-1=0.9544$$
$$P\lbrace \mu-3\sigma < X \leq \mu + 3\sigma\rbrace=\Phi(3)-\Phi(-3)=2\Phi(3)-1=0.9974$$
由此可知,虽然正太变量的取值范围是$(-\infty,+\infty)$,但是它的值基本落在$(\mu-3\sigma,\mu+3\sigma)$中,即“$3\sigma$”法则。
2.3 上$\alpha$分位点
为了便于数理统计上的应用,对于标准正太变量,引入上$\alpha$分位点的定义。
设$X\sim N(0, 1)$,若$z_{\alpha}$满足条件
$$P\lbrace X>z_{\alpha}\rbrace=\alpha, \quad 0<a<1$$
则称点$z_{\alpha}$为标准正太分布的上$\alpha$分位点,如下图所示。
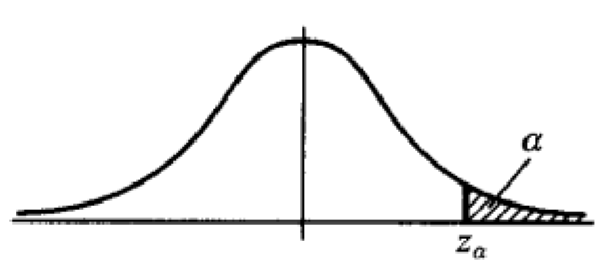
下面是几个常用的$z_{\alpha}$的值。
| $\alpha$ | 0.001 | 0.005 | 0.01 | 0.025 | 0.05 | 0.10 |
|---|---|---|---|---|---|---|
| $z_{\alpha}$ | 3.090 | 2.576 | 2.326 | 1.960 | 1.645 | 1.282 |
由$\varphi(x)$图形的对称性可知,$z_{1-\alpha}=-z_{\alpha}$。
2.4 正太分布的一些性质
- 如果$X\sim N(\mu, \sigma^2)$且a与b都是实数,那么$aX+b\sim N(a\mu+b, (a\sigma)^2)$;
- 如果$X\sim N(\mu_X, \sigma^2_X)$与如果$Y\sim N(\mu_Y, \sigma^2_Y)$是相互独立的正太随机变量,则:
- 它们的和满足正太分布$U=X+Y\sim N(\mu_X+\mu_Y,\sigma^2_X +\sigma^2_Y)$;
- 它们的差满足正太分布$U=X-Y\sim N(\mu_X-\mu_Y,\sigma^2_X +\sigma^2_Y)$;
- U与V两者是相互独立的。(要求X与Y的方差相等?)
- 如果$X_1,…,X_n$为独立标准正太随机变量,那么$X^2_1+\cdots +x^2_n$服从自由度为n的卡方分布。
- 正太分布是无限可分的概率分布。
2.5 中心极限定理
正态分布有一个非常重要的性质:在特定条件下,大量统计独立的随机变量的平均值的分布趋于正态分布,这就是中心极限定理。中心极限定理的重要意义在于,根据这一定理的结论,其他概率分布可以用正态分布作为近似。
- 参数为n和p的二项分布,在n相当大且p接近于0.5的时候近似于正太分布,近似正太分布平均数为$\mu=np$且方差为$\sigma^2=np(1-p)$;
- **泊松分布带有参数 $\lambda$ 当取样样本数很大时将近似正态分布$\lambda$**,近似正态分布平均数为$ \mu = \lambda$且方差为 $\sigma^2 = \lambda$。
参考文献
- 应该如何理解概率分布函数和概率密度函数?
- 《浙江大学概率论与数理统计》盛骤等
- 正态分布

