深度学习调参初级版
今天介绍一些深度学习调参的初级经验。其实知乎上已经有相关问题了,见《 深度学习调参有哪些技巧?》,这里总结一下,并做一些补充。对于初学者来说,深度学习调参有几个比较重要的参数。学习率,损失函数,层大小,参数正则化,参数初始化的分布,优化函数,模型深度,dropout,batch大小。先引入量子位的一张图:
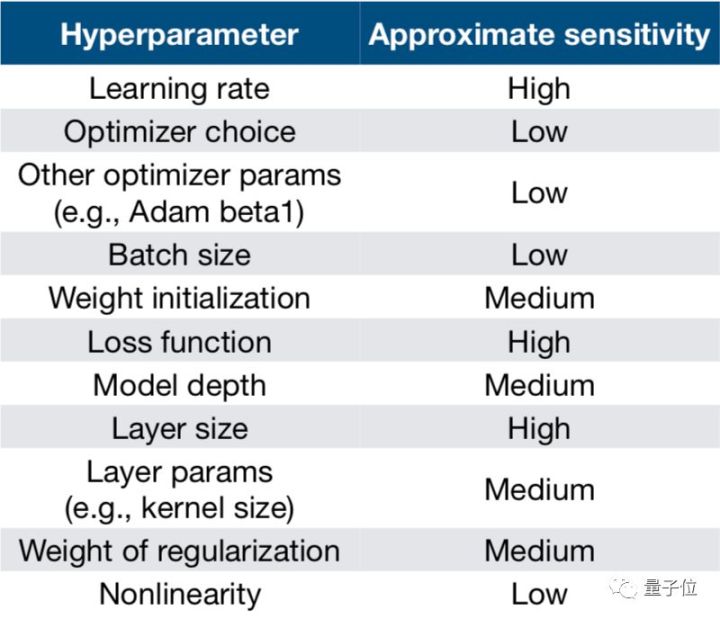
1 学习率
学习率是深度学习调参中一个比较重要的参数,其决定了模型收敛的速度,以及是否可以收敛到极值。学习率很大模型收敛地很快,但是收敛到一定程度模型容易发生震荡,无法达到极值点;将学习率设置很大也容易导致loss变成Nan。如果学习率设置地很小,模型会训练地比较慢,也可能落入局部极小值。
一般学习率可以从0.1或0.01开始尝试。大多数情况下,使用衰减学习率有助于模型训练,在TF中实现了学习率的指数衰减函数 tf.train.exponential_decay()。函数原型如下:
1 | tf.train.exponential_decay( |
上述函数实现了如下功能:
1 | decayed_learning_rate = learning_rate * |
举个例子:
1 | global_step = tf.Variable(0, trainable=False) |
上述代码指定了staircase=True,所以每训练100轮后学习率乘以0.96。
2. 损失函数
TF既支持经典的损失函数,也支持自定义损失函数。一般用的交叉熵,别的损失函数没有怎么实践过。
3. 参数正则化
一般使用L2正则化对权重和偏置参数做限制,通过函数 tf.nn.l2_loss 实现。具体用法:
1 | regularizers = tf.nn.l2_loss(weights['h1']) + tf.nn.l2_loss(biases['b1']) |
L2正则的beta参数可以设置0.0001,也可以尝试下0.001。
4. 层大小
知道这个有影响,但是还没有摸索出什么经验。
5. 参数初始化的分布
参数初始化一般就是高斯分布/均匀分布,但是在使用上述两种方式初始化时,可以采用一定的技巧,引用知乎用户萧瑟的回答:
- uniform均匀分布初始化:
w = np.random.uniform(low=-scale, high=scale, size=[n_in,n_out])
- Xavier初始法,适用于普通激活函数(tanh,sigmoid):scale = np.sqrt(3/n)
- He初始化,适用于ReLU:scale = np.sqrt(6/n)
- normal高斯分布初始化:
w = np.random.randn(n_in,n_out) * stdev # stdev为高斯分布的标准差,均值设为0
- Xavier初始法,适用于普通激活函数 (tanh,sigmoid):stdev = np.sqrt(n)
- He初始化,适用于ReLU:stdev = np.sqrt(2/n)svd初始化:对RNN有比较好的效果。参考论文:https://arxiv.org/abs/1312.6120
Xavier初始法论文:http://jmlr.org/proceedings/papers/v9/glorot10a/glorot10a.pdf
He初始化论文:https://arxiv.org/abs/1502.01852
- Xavier初始化
基本思想是:保持输入和输出的方差一致,这样就避免了所有输出值都趋向于0 - He初始化
基本思想是:在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0,所以,要保持variance不变,只需要在Xavier的基础上再除以2。 详细可以看下这篇文章《聊一聊深度学习的weight initialization》,讲的挺好的。
大多数情况下使用上述初始化方式已足够,但是也有例外。有人使用全0初始化取得了不错的效果,所以参数初始化并没有什么固定的结论,多尝试下吧。一般来说,良好的初始化可以让参数更加逼近最优解,大大提高收敛速度,防止局部最小。
另外,TF的随机数生成函数如下表所示:
| 函数名称 | 随机数分布 | 主要参数 |
|---|---|---|
| tf.random_normal | 正太分布 | 平均值,标准差,取值类型 |
| tf.truncated_normal | 正太分布,但如果随机出来的值偏离平均值超过2个标准差,则重新随机 | 平均值,标准差,取值类型 |
| tf.random_uniform | 均匀分布 | 最小、最大取值、 取值类型 |
| tf.random_gamma | Gamma 分布 | 形状参数、尺度参数beta,取值类型 |
1 | tf.Variable(tf.random_normal([gender_emlen], stddev=std)) |
TF也支持通过常数初始化一个变量,下表是常用的常量声明方法:
| 函数名称 | 功能 | 样例 |
|---|---|---|
| tf.zeros | 产生全0的数组 | tf.zeros([2,3], int32) -> [[0,0,0],[0,0,0]] |
| tf.ones | 产生全0的数组 | tf.ones([2,3], int32) -> [[1,1,1],[1,1,1]] |
| tf.fill | 产生全为给定数字的数组 | tf.fill([2,3],9) -> [[9,9,9],[9,9,9]] |
| tf.constant | Gamma 分布 | tf.constant([1,2,3] -> [1,2,3]) |
6. 优化函数
我目前使用adam函数多一些,据说adam在大多数场景表现良好。另外,sgd +momentum据说也不错?
7. 模型深度
在工业上一般使用浅层模型,我一般尝试不超过4层网络,多了效果通常不太理想,收敛太慢。
8. dropout
dropout一般设置0.4-0.6,通常设置0.5,这样网络变化最大。但是也不是绝对的。
9. batch大小
之所以神经网络模型会分batch训练,是因为当数据集很大时内存放不下,而一条一条数据集进行训练会导致模型震荡不收敛,所以选择了一个折中方案,即批训练。
增大batch的好处:
- 内存利用率提高,每个epoch训练的轮次减少,训练相同的数据量时间更短;
- 一定范围内,提高batch可以使得模型训练更稳定,不至于严重震荡(相对地,参数更新相对更慢,达到相同精度所需要的时间增加)。
增大batch可能引起的问题:
- 内存不够;
- 跑完一个epoch的轮次减少,达到相同精度所需要的epoch次数增加,即增加了训练时间;
- batch增大到一定程度,其下降方向基本不再变化;
- 过大的batch会大大降低了下降的随机性,模型可能达到局部极小值,精度降低;
- 过大的batch会大大降低了下降的随机性,模型的泛化性能可能会下降,见知乎用户龙鹏-言有三的回答。
知乎用户龙鹏-言有三还给出了两个建议:
- 如果增加了学习率,那么batch size最好也跟着增加,这样收敛更稳定。
- 尽量使用大的学习率,因为很多研究都表明更大的学习率有利于提高泛化能力。如果真的要衰减,可以尝试其他办法,比如增加batch size,学习率对模型的收敛影响真的很大,慎重调整。
对于batch大小的取值,知乎用户夕小瑶也给出的自己的经验:
对于SGD(随机梯度下降)及其改良的一阶优化算法如Adagrad、Adam等是没问题的,但是对于强大的二阶优化算法如共轭梯度法、L-BFGS来说,如果估计不好一阶导数,那么对二阶导数的估计会有更大的误差,这对于这些算法来说是致命的。
因此,对于二阶优化算法,减小batch换来的收敛速度提升远不如引入大量噪声导致的性能下降,因此在使用二阶优化算法时,往往要采用大batch哦。此时往往batch设置成几千甚至一两万才能发挥出最佳性能。
另外,听说GPU对2的幂次的batch可以发挥更佳的性能,因此设置成16、32、64、128…时往往要比设置为整10、整100的倍数时表现更优(不过我没有验证过,有兴趣的同学可以试验一下~)

