《Network Pruning via Transformable Architecture Search》论文阅读
网络修剪可减少过度参数化的网络的计算成本,而不会影响性能。现有的修剪算法会预先定义修剪网络的宽度和深度,然后将参数从未修剪的网络传输到修剪的网络。为了突破修剪网络的结构限制,我们提出应用神经架构搜索(NAS)直接搜索具有灵活的通道大小和层大小的网络。通过最小化修剪网络的损失来学习通道/层的数量。修剪后的网络的特征图是K个特征图片段的集合(由不同大小的K个网络生成),这些片段是根据概率分布进行采样的。损耗不仅可以反向传播到网络权重,还可以反向传播到参数化分布,以显式调整通道/层的大小。具体来说,我们应用逐通道插值(填充)以使具有不同通道大小的特征图在聚合过程中保持对齐。每个分布中的size的最大概率用作修剪网络的宽度和深度,修剪网络的参数是通过知识迁移(例如知识蒸馏)从原始网络中获知的。与传统的网络修剪算法相比,在CIFAR-10,CIFAR-100和ImageNet上进行的实验证明了我们的网络修剪新观点的有效性。进行了各种搜索和知识转移方法以显示这两个组件的有效性。代码位于:https://github.com/D-X-Y/NAS-Projects
1 介绍
深度卷积神经网络(CNN)正在变得更宽更深,以在不同的应用程序上实现高性能[17、22、48]。 尽管它们取得了巨大的成功,但将它们部署到资源受限的设备(如移动设备和无人机)上并不可行。 解决该问题的一个直接方案是使用网络修剪[29、12、13、20、18]来减少过参数化CNN的计算成本。 如图1(a)所示,用于网络修剪的典型pipeline是通过删除冗余过滤器,然后基于原始网络微调修剪网络来实现的。基于滤波器重要性的不同技巧被使用,例如滤波器的L2范数[30],重构误差[20]和可学习的缩放因子[32]。最后,研究人员对修剪后的网络应用了各种微调策略[30,18],以有效地传递未修剪网络的参数并最大化修剪后的网络的性能。
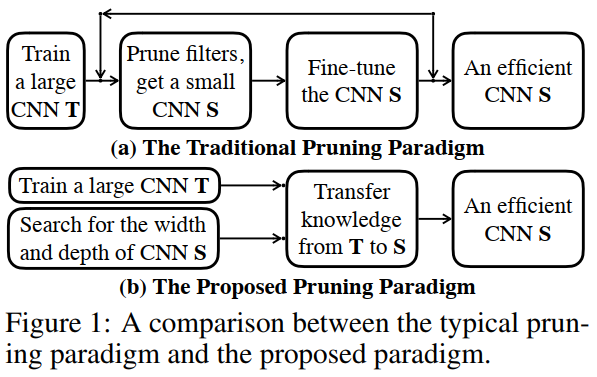
传统的网络修剪方法在保持准确性的同时,对网络进行了有效地压缩。它们的网络结构是直观设计的,例如,在每一层中裁减30%的滤波器[30、18],预测稀疏率[15]或利用正则化[2]。修剪后的网络精度受限于人工设计的结构或结构规则。为了克服这个限制,我们使用神经架构搜索(NAS)将架构设计转变为学习过程,并提出了一种新的网络修剪范例,如图1(b)所示。
现有的NAS方法[31、48、8、4、40]优化了网络拓扑,而本文的重点是自动网络规模。为了满足要求并公平地比较以前的修剪策略,我们提出了一种称为可迁移架构搜索(TAS)的新NAS方案。** TAS旨在搜索最佳网络规模而不是拓扑,通过最小化计算成本进行正则化(浮点操作FLOPs)。然后,通过知识迁移来学习搜索/修剪网络的参数**[21、44、46]。
TAS是一种可微分的搜索算法,可以有效且高效地搜索网络的宽度和深度。具体而言,不同的候选通道/层以可学习的概率被添加到网络中。通过反向传播修剪网络产生的损失来学习概率分布,修剪后网络的特征图是根据概率分布采样的K个特征图片段(不同大小的网络输出)的集合。这些不同通道大小的特征图借助通道插值方式进行汇总。每个分布中概率最大的size用作修剪网络的宽度和深度。
在实验中,我们证明,通过知识蒸馏(KD)传递参数的搜索架构优于之前在CIFAR-10,CIFAR-100和ImageNet上的修剪方法。我们还对传统的人工修剪方法[30,18]和随机架构搜索方法[31]生成的架构测试了不同的知识迁移方法。对不同架构的相同改进证明了知识迁移的普遍性。
2 相关工作
网络修剪[29,33]是压缩和加速CNN的有效技术,因此允许我们在存储和计算资源有限的硬件设备上部署有效的网络。已经提出了多种技术,例如低秩分解[47],权重修剪[14、29、13、12],通道修剪[18、33],动态计算[9、7]和量化[23, 1]。它们有两种模式:非结构化修剪[29、9、7、12]和结构化修剪[30、20、18、33]。
非结构化修剪方法[29、9、7、12]通常会 **强制卷积权重[29、14]或特征图[7、9]稀疏**。非结构化修剪的先驱 LeCun等[29]和Hassibi等[14]研究了使用二阶导数信息来修剪浅层CNN的权重。在深度网络于2012年诞生后[28],Han等人[12,13,11]提出了一系列基于L2正则化获得高度压缩的深度CNN的工作。经过这一发展,许多研究人员探索了不同的正则化技术来提高稀疏度,同时又保持了准确性,例如L0正则化[35]和输出灵敏度[41]。由于这些非结构化方法使大型网络稀疏而不是改变网络的整体结构,因此它们需要针对依赖项的专用设计[11]和特定的硬件来加快推理过程。
结构化修剪方法[30、20、18、33]的目标是 **对卷积过滤器或所有层进行修剪**,因此可以轻松开发和应用修剪后的网络。该领域的早期工作[2,42]利用组Lasso来实现深度网络的结构化稀疏性。之后,李等人[30]提出了典型的三阶段修剪范例(训练大型网络,修剪,再训练)。这些修剪算法将具有较小范数的过滤器视为不重要,并且倾向于修剪它们,但是这种假设在深层非线性网络中不成立[43]。因此,许多研究人员专注于信息过滤器的更好标准。例如,刘等[32]利用L1正则化;Ye等[43]对ISTA施加了惩罚(applied a ISTA penalty);He等[19]利用了基于几何中位数的标准。与以前的修剪pipeline相反,我们的方法允许显式优化通道/层的数量,从而使学习到的结构具有高性能和低成本。
除了信息过滤器的标准,网络结构的重要性在[33]中被提出。通过自动确定每一层的修剪和压缩率,某些方法可以隐式地找到特定于数据的架构[42、2、15]。相比之下,我们使用NAS明确发现了该架构。先前的大多数NAS算法[48、8、31、40]会自动发现神经网络的拓扑结构,而我们专注于搜索神经网络的深度和宽度。基于强化学习(RL)的[48,3]方法或基于进化算法的[40]方法可以搜索具有灵活宽度和深度的网络,但是它们需要大量的计算资源,因此无法直接用于大规模目标数据集。可微分的方法[8,31,4]显着降低了计算成本,但它们通常假定不同搜索候选集的通道数相同。 TAS是一种可微分的NAS方法,它能够有效地搜索具有灵活宽度和深度的迁移网络。
网络迁移(Network transformation)[5,10,3]也研究了网络的深度和宽度。 Chen等[5]手动拓宽和加深网络,并建议使用Net2Net初始化更大的网络。 Ariel等[10]提出了一种启发式策略,通过在缩小和扩展之间交替来找到合适的网络宽度。蔡等[3]利用RL代理来增加CNN的深度和宽度,而我们的TAS是一种可微分的方法,不仅可以扩大CNN,而且可以缩小CNN。
在网络修剪相关的文献中,知识迁移已被证明是有效的。网络的参数可以从预训练的初始化[30,18]中迁移。Minnehan等[37]通过逐块重构损失来迁移未压缩网络的知识。在本文中,我们应用了一种简单的KD方法[21]来进行知识转移,从而使架构搜索具有良好的性能。
3 方法
我们的修剪方法包括三个步骤:(1)通过标准分类训练程序训练未修剪的大型网络。 (2)通过TAS搜索小型网络的深度和宽度。(3)通过简单的KD方法将知识从未修剪的大型网络迁移到搜索得到的小型网络[21]。 下面将介绍背景知识,TAS的详细信息,并说明知识迁移过程。
3.1 迁移架构搜索
网络通道修剪旨在减少网络每一层中的通道数量。 给定输入图像,网络会将其作为输入,并在每个目标类别上产生概率。 假设$X$和$O$是第$l$个卷积层的输入和输出特征张量(我们以3×3卷积为例),该层计算过程如下:
$$
O_j=\sum_{k=1}^{c_{in}}{X_k,:,: \ast W_{j,k},:,:} \qquad where ; 1\leq j \leq c_{out} \tag{1}
$$
其中$W\in R^{c_{out\times c_{in} \times 3 \times 3}}$表示卷积核权重,$c_{in}$为输入通道,$c_{out}$为输出通道。 $W_{j,k,:,:}$对应第$k$个输入通道和第$j$个输出通道。$\ast$表示卷积运算。 通道修剪方法可以减少$c_{out}$的数量,因此,也减少了下一层的$c_{in}$。
搜索宽度 我们使用参数$\alpha \in R^{|C|}$来表示一层中可能的通道数分布,其中,$max(C)≤c_{out}$。 选择通道数量的第$j$个候选的概率可以表示为:
$$
p_j=\frac{exp(\alpha_j)}{\sum_{k=1}^{|C|}{exp(\alpha_k)}} \qquad where; 1\leq j \leq |C| \tag{2}
$$
但是,**上述过程中的采样操作是不可微的**(可以参考《Gumbel-Softmax的采样技巧》),这阻止了我们将梯度从$p_j$反向传播到$\alpha_j$。 受[8]的启发,我们应用Gumbel-Softmax [26,36]来软化采样过程以优化$\alpha$:

其中$U(0,1)$表示0和1之间的均匀分布。$\tau$是softmax温度参数。 当$\tau \to 0$时,$\hat{p}=[\hat{p}_1,…,\hat{p}_j,…]$变为one-shot?(此处暂时没想明白,可以参考《Gumbel-Softmax 对离散变量再参数化》),并且基于$\hat{p}$的Gumbel-softmax分布与类别分布相同。当$\tau \to \infty$,Gumbel-softmax分布在$C$上变为均匀分布。我们方法中的特征图定义为具有不同大小的原始特征图片段的加权和,其中权重为$\hat{p}$。 通过逐通道插值(CWI)对齐具有不同大小的特征图,以便计算加权和。 为了减少内存成本,我们选择索引$I\subseteq[|C|]$为的小子集进行聚合,而不是使用所有channel候选集( **此处提出了针对形如等式2中的概率计算不可微问题可以采取的策略,即使用Gumbel-Softmax进行软化 **)。此外,权重根据所选size的概率重新归一化,公式如下:

其中$\tau_{\hat{p}}$表示由$\hat{p}$参数化的多项式概率分布。CWI是将不同尺寸的特征图对齐的一般操作。它可以通过多种方式实现,例如空间迁移网络( spatial transformer network)的3D变体[25]或自适应池操作[16]。在本文中,我们选择3D自适应平均池化操作[16]作为${CWI}^2$,因为它没有带来额外的参数并且可以忽略不计的额外成本。我们在CWI之前使用批规范化[24]来规范化不同的片段。图2以$|I|=2$为例阐述了上述过程。
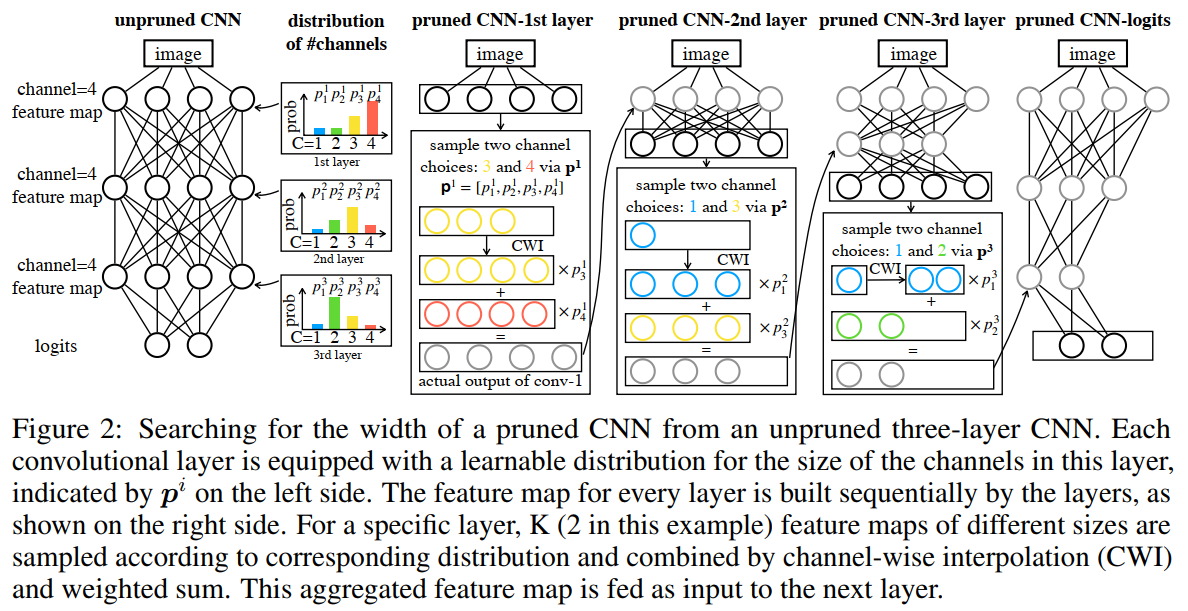
需要注意的是,$I=2$表示有两个 channel 值不同的卷积核进行CWI。具体做法如下:
1 | if self.avg : out = self.avg( inputs ) |
而conv_forward中是怎么实现的呢?
1 | def conv_forward(inputs, conv, choices): |
看15行,也就是说先按照候选 channel 的最大值进行卷积,然后根据候选 channel 使用切片进行获取。这样就金额以方便地获取不同 channel 对应的卷积输出。
讨论等式4中的抽样策略 $\quad$ 该策略旨在仅仅通过反向传播采样架构的梯度(而不是整个架构),将内存成本和训练时间减少到可接受的数量。与通过均匀分布采样相比,所应用的采样方法(基于概率的采样)可以减弱多次迭代后每次迭代采样所导致的梯度差。
搜索深度 我们使用参数来表示具有$L$个卷积层的网络中可能的层数分布。我们使用和等式3类似的策略来采样层数。并使用深度为$l$的采样分布$\hat{q}_l$使$\beta$与$\alpha$可微分。然后,对于所有可能的深度,我们计算出修剪后的网络的最终输出特征,进行汇总,其表示为:

其中$\hat{O^l}$表示在等式4中第$l$层的输出特征图。$C_{out}$表示所有$\hat{O^l}$中的最大采样通道。 将最终输出的特征图$O_{out}$喂入最后的分类层以进行预测。 这样,我们可以将梯度反向传播到宽度参数$\alpha$和深度参数$\beta$。
搜索目标 最终的架构$A$是通过选择具有最大概率的候选项而得出的,该候选项由架构参数(等式8中形如$A$的字符即表示架构参数,此处不知如何书写)获知,该架构参数由每层的$\alpha$和$\beta$组成。 我们的TAS的目标是通过将训练损失$\zeta_{train}$最小化,找到经过训练后具有最小验证损失$\zeta_{val}$的架构$A$:
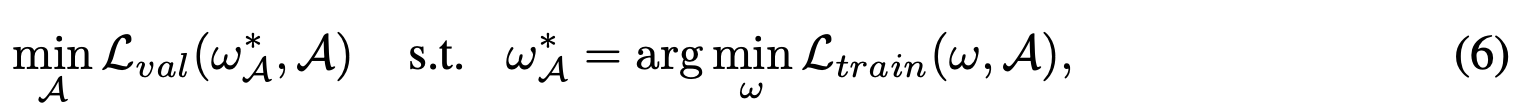
其中$w_A^{\ast}$表示$A$的优化权重。训练损失是网络的交叉熵分类损失。 现有的NAS方法[31、48、8、4、40]通过具有不同拓扑的网络候选项优化$A$,而我们的TAS则是搜索具有相同拓扑结构以及较小宽度和深度的候选项。 所以,我们搜索过程中的验证损失不仅包括分类验证损失,还包括计算成本的惩罚:

其中$z$是一个向量,表示修剪后网络的输出对数,$y$表示相应输入的真实类别,而$\lambda_{cost}$是$\zeta_{cost}$的权重。 成本损失会促使网络的计算成本(例如FLOP)收敛到目标R,以便可以通过设置不同的$R$来动态调整成本。我们使用的分段计算成本损失如下:
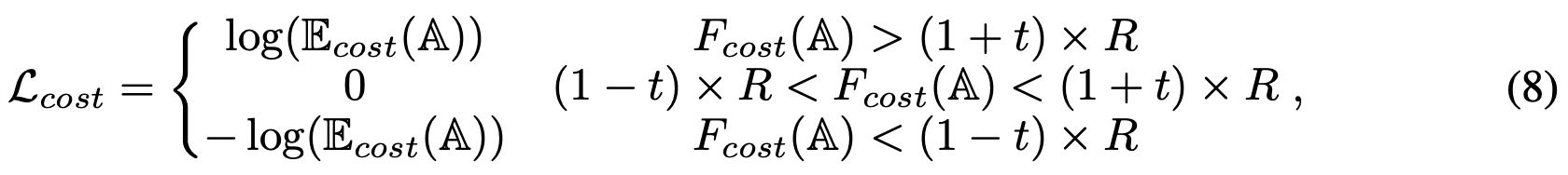
其中$E_{cost}(A)$基于架构参数$A$计算期望的计算成本。具体地说,它是所有候选网络的计算成本的加权总和,其中权重是采样概率。$F_{cost}(A)$表示搜索到的架构的实际成本,其宽度和深度从$A$得出。$t\in [0,1]$表示容忍度,它减慢了更改搜索架构的速度。需要注意的是,我们使用FLOP来评估网络的计算成本,并且很容易用其它度量标准(例如延迟[4])来代替FLOP。
我们在Alg1中展示了整个算法。在搜索过程中,我们使用等式5迁移网络,使权重和架构参数可区分。我们也可以在训练集上最小化$\zeta_{train}$来优化修剪的网络的权重,而在验证集上最小化$\zeta_{val}$来优化架构参数$A$。搜索之后,我们以最大的概率选择通道数作为宽度,以最大概率选择层数作为深度。最终搜索的网络由选定的宽度和深度构成。该网络将通过KD进行优化,我们将在3.2小结中详细介绍。

3.2 知识迁移
知识迁移对于学习健壮的修剪网络非常重要,我们在搜索的网络架构上采用了简单的KD算法[21]。 此算法鼓励小型网络的预测$z$通过以下目标,与未修剪网络的软目标匹配:
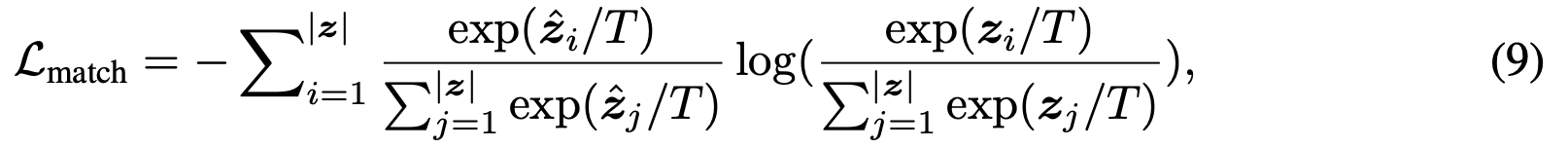
其中$T$是温度参数,$\hat{z}$表示来自预训练的未修剪网络的logit输出向量。 此外,它使用带有交叉熵损失的softmax来鼓励小型网络预测真实目标。 KD的最终目标如下:

其中$y$表示相应输入的真实目标类别。$\lambda$是平衡标准分类损失和软匹配损失的损失权重。 在搜索到目标网络(第3.1节)之后,我们首先对未修剪的网络进行预训练,然后通过等式10从未修剪的网络迁移来优化搜索到的网络。
实验部分见下文。

