cross特征总结
cross特征是机器学习中一类非常有用的特征,例如在推荐系统领域,用户和商品的交叉特征往往可以给模型带来极大的增益,例如<性别女, 口红>的交叉特征,当一个用户是女性且商品是口红时,点击的概率就会很高;反之<男,口红>点击的概率就很低了。下面总结一些cross特征相关的工作,比较典型有FM, FFM, 各类NN模型等。DNN模型不在文本讨论之列,DNN的全连接层带交叉特征的能力,但是有些情况下我们需要构造一些更加直接的cross特征。
1 人工构造二阶交叉特征
FM是人工构造二阶交叉特征的代表。FM诞生之初是为了解决稀疏数据下的特征组合问题。多项式模型是包含特征组合最直观的模型,在多项式模型中,特征$x_i$和$x_j$的组合采用$x_ix_j$表示,即当$x_i$和$x_j$都非零时,组合特征$x_ix_j$才有意义。以二阶多项式模型为例,其表达式如下:
$$
y(x)=w_0 + \sum^n_{i=1}w_ix_i + \sum^n_{i=1}\sum^n_{j=i+1}w_{ij}x_ix_j
$$
在数据普遍稀疏的情况下,二次项参数$w_{ij}$训练时很困难的。基于模型的协同过滤中,一个评分矩阵通常被分解为user矩阵和item矩阵的积(MF),每个user向量和每个item向量的点积就表示了这个user对这个item的评分。

借鉴于上述思路,同时也是对称矩阵的二次项参数$w_{ij}$可以分解为两个矩阵的乘积,即$W=V^TV$,$V$的第 $j$ 列表示第 $j$ 维特征的隐向量。因此二阶cross特征的FM模型方程为:
$$
y(x)=w_0 + \sum^n_{i=1}w_ix_i + \sum^n_{i=1}\sum^n_{j=i+1}v_iv_j^Tx_ix_j
$$
2 自动构造有限高阶的交叉特征
论文《Deep & Cross Network for Ad Click Predictions》是斯坦福和Google合作的一篇论文,论文中提出了一种自动构造有限高阶交叉特征的方法,并且使构造交叉特征的层拟合残差。网络结构如下:
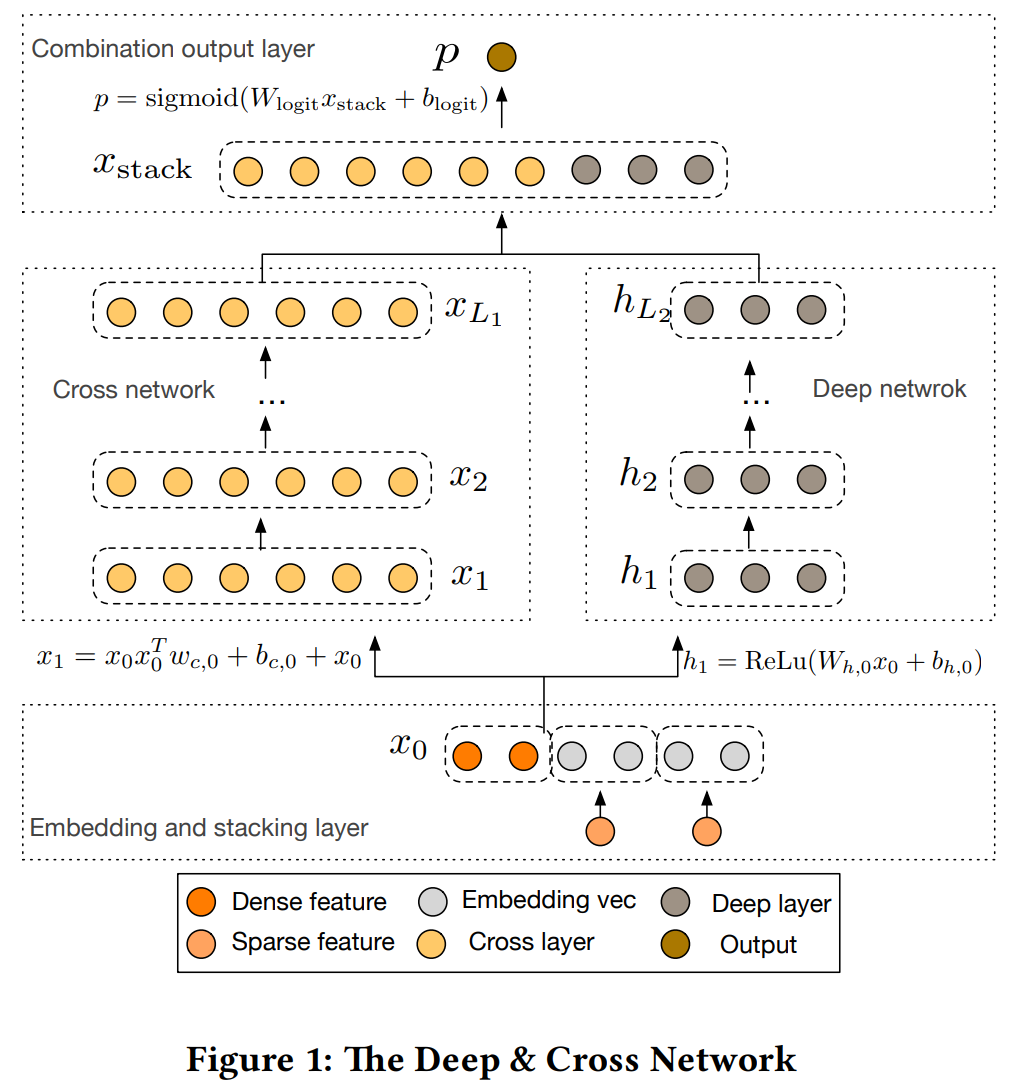
模型的输入有稀疏特征和稠密特征,稀疏特征embedding之后和归一化后的稠密特征concat,一起作为cross网络和deep网络的输入。deep网络就是简单的全连接层,cross网络拟合了残差 $x_{i+1}-x_i$,目的是使得网络更深;并且可以注意到cross网络的输入和输出的维度是相同的。可以看下cross是如何进行的:
$$
x_1=x_0x_0^Tw_{c,0} + b_{c,0} + x_0
$$
下面的图就非常直观地展示了cross机制:

关于这个模型的总结,知乎已经有大佬总结的很到位了《揭秘 Deep & Cross : 如何自动构造高阶交叉特征》。


